This week I updated my code so that it’s easier to use. Now one can refer to a specific note and get its frequency as easy as this:
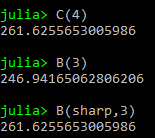
And those numbers can be used as inputs to the visualizer, like this:
image = harmony_vis( nothing, B(flat, 4), D(5), F(5) );
save("B_flat_major.png", image)
image = harmony_vis( B(flat, 2), B(flat, 4), D(5), F(5) );
save("B_flat_major_over_B_flat_base_note.png", image)That is also an example of how the function can be used to create those images of either three-note or four-note chords. If the first input is nothing (that’s a Julia object that represents nothing or no data, equivalent to Python’s None), then the visualizer will produce a two-rowed picture ( from the next three inputs. Otherwise, the first input will be used as the root note for a four-rowed picture. In either case, the three inputs after the first will be coloured red, green, and blue, respectively.
Here is a link to my Julia code.
Because this system made it clear what notes I was using, I realized some of the images from last week were using notes higher or lower than I had said, and many were labelled wrong in the gallery. I have since fixed those.
As well as four-note chords, I noticed this visualization scheme can be used to look at functional harmony, relating some three-note chord back to a “tonal center.” In the following gallery you can see how the main six diatonic chords in the key of C overlap with the harmonic series of C2. I have used inversions of the chords to keep them within a close pitch-range of one another. Also, I am assuming from prior work that, in a major key, what we hear as the tonal center is the note two octaves below the root of the I (one) chord. Conventionally because of the phenomenon of “octave equivalence,” we would just say that the tonal center is C. However, I am theorizing that the particular note is significant, that higher and lower ‘C’s are harmonically close to the tonal center, but distinct from it.






A nice thing about this collection is it shows all of the close-position inversions of major and minor chords. For next week I will keep looking for patterns in here, and focus on this functional harmony. Questions: Can this show us how a major key works? What about a minor key? What might this say about “borrowed chords?”
Also, I have noticed that this analysis can be easily generalized to notes outside the normal tuning (microtonal notes). So I will like to try using it to find nice-sounding microtonal harmonies, make a composition, and create some audio for that.
